今回は、複数の電池や抵抗を横に並べて(並列)つないだとき(並列接続) に、回路がどのような性質を持つのかを紹介します。
並列接続とは
複数の抵抗を横に並べて接続することを、抵抗の並列接続といいます。
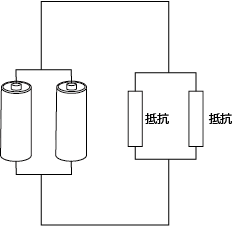
抵抗の並列接続
水の回路でたとえると、1本のホースよりも複数のホースがある方が、より多くの水を流すことができます。
これは、流れる道が増えると、全体として水が流れやすくなる(抵抗が小さくなる) ためです。
電気も同じで、抵抗を並列に接続すると、電気回路全体の抵抗は小さくなり、電池から流れる電流が増加します。
また、並列接続には重要な特徴があります。
- 並列に接続された抵抗には、すべて同じ電圧がかかる
- 流れる電流は分かれて、それぞれの抵抗に別々の量が流れる
電池の並列接続
電池の並列接続では、各電池が電流を分担するので、電池の連続動作時間が長くなります。
例えば、抵抗Rが3[Ω]の電球に電圧Vが1.5[V]の電池を1つ接続すると、電池に流れる電流Iは、
電流I[A]=電圧V[V]÷抵抗R[Ω]
より、0.5[A]になります。
同じ電池をもう1つ並列接続しても、電圧も抵抗も同じなので、電流は0.5[A]です。
ただし、2つの電池から電流が流れるため、各電池から流れる電流は0.25[A]になります。
このように、電流が分担されるため、結果として電池を長時間使うことができるようになります。
ここでは説明を分かりやすくするため、内部抵抗などは考慮していません。
並列接続の合成抵抗
並列接続では、それぞれの抵抗にかかる電圧は同じです(どちらも電池の電圧V)
抵抗R1に流れる電流I1=電圧V÷抵抗R1、
抵抗R2に流れる電流I2=電圧V÷抵抗R2
です。
また、それぞれの抵抗に流れる電流を合計したものが、全体の電流になります。
全体電流I=電流I1+電流I2
これを式で整理すると、
全体電流I(電圧V÷抵抗R)=電流I1(電圧V÷抵抗R1)+電流I2(電圧V÷抵抗R2)
電圧 V は共通の値なので両辺から消すことができ、次の式になります。
(1÷抵抗R)=(1÷抵抗R1)+(1÷抵抗R2)
となります。
つまり、合成抵抗Rの逆数が、各抵抗の逆数の合計になる ということです。
さらに一般化すると、抵抗が3つ以上の場合は次のようになります。
1 ÷ R = 1 ÷ R1 + 1 ÷ R2 + 1 ÷ R3 + …
例えば、R1=6Ω、R2=3Ω の合成抵抗は次のようになります。
1 ÷ R = 1 ÷ 6 + 1 ÷ 3
1 ÷ R = 1 ÷ 6 + 2 ÷ 6
1 ÷ R = 3 ÷ 6
1 ÷ R = 1 ÷ 2したがって、
R = 2Ωなお、並列接続の特徴として、「合成抵抗は、接続された抵抗の中で最も小さい値よりもさらに小さくなる」という重要な性質があります。
(今回の場合、最も小さな抵抗は、3Ω ですが、合成抵抗は 2Ω になっています。)
まとめ
- 並列接続とは、抵抗や電池を横に並べてつなぐ接続方法。
- 水の流れの例のように、流れる道が増えるため 全体の抵抗は小さくなる。
- 並列接続された抵抗には 同じ電圧 がかかる。
- 流れる電流は それぞれの抵抗に分かれて流れる。
- 合成抵抗 R は、
1/R = 1/R1 + 1/R2 + … の式で求められる。 - 合成抵抗は、接続された抵抗の中で 最も小さい抵抗値よりもさらに小さくなる。
- 電池の並列接続では、電圧は 変わらず同じまま。
- 電流は複数の電池で 分担されるため、1本のときより長く使える。
